本节书摘来自华章计算机《编写高质量代码：改善c程序代码的125个建议》一书中的第1章，建议3-4,作者：马　伟 更多章节内容可以访问云栖社区“华章计算机”公众号查看。

建议3-4：避免直接在浮点数中使用“==”操作符做相等判断

在整型数据中，我们一般都使用“==”操作符来判断两个数是否相等。在浮点数据的运算中，也存在着“==”操作符，那么是否也可以使用这个“==”操作符来判断两个浮点数是否相等呢？带着这个问题，示例程序如代码清单1-21所示。

代码清单1-21　浮点数相等判断示例#include 
    
     int main(void){     float f1=3.46f;    float f2=5.77f;    float f3=9.23f;     printf("f1(3.46f)=%0.20f\nf2(5.77f)=%0.20f\nf1+f2=%0.20f\n            f3(9.23f)=%0.20f\n",f1,f2,f1+f2,f3);    if(f1+f2==f3)    {            printf("f1+f2==f3\n");    }    else    {            printf("f1+f2!=f3\n");    }           return 0;   }
    

在代码清单1-21中，分别定义了3个float变量 f1、f2与f3。从表面上看，f1+f2的值应该是9.23，因此执行条件判断语句“if(f1+f2==f3)”时，应该返回true。但实际的运行结果并非如此，如图1-33所示。

要想使语句“if(f1+f2==f3)”返回true，那么f1+f2和f3在浮点格式的精度限制内必须严格相等。这也就意味着，一般情形下（0除外），浮点格式中的每一个位都必须相等。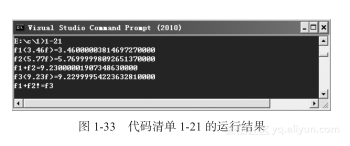

由于浮点数存在误差，即使是同一意义上的值，如果来源不同，那么判断也就可能不会为true。换句话说，在浮点计算中，“==”的作用是比较两个浮点数是否具有完全相同的格式数据，而不是一般数学或工程意义上的相等。在浮点计算中两个数据相等的含义通常是指在误差范围内，两个数据的意义一致（即二者描述的物理量的取值一致，或者说相容），因此不能使用“==”操作符进行判断。

既然不能使用“==”操作符进行判断，那么我们又应该怎样正确判断两个浮点数是否相等呢？一般情况下，浮点数的相等判断通常使用如下形式，即：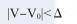

示例代码如下所示：

if(fabs(a-b) < epsilon)

其中，epsilon是一个绝对的数据。采用这种形式来判断相等，很显然，如何确定Δ就成了问题的关键所在。Δ值的确定需要考虑数值背后的含义，而且它总是与误差的概念相随。

（1）依据数据误差进行判断如果两个数据相差Δ，假设一个数据的误差是Δ1，另一个数据的误差是Δ2，那么一个简单的判据是：

实际上，如果数据不是直接来自某个测量设备，而是某个仿真系统的输出或者是测量数据经过一系列处理的结果，那么Δ1和Δ2大多没有确定的值。此外，这种方法在理论上也不够严谨，只是便于使用而已。 （2）依据允许误差进行判断 在许多情况下，计算精度和数据精度均远远超过了实际需求，使用数据误差进行相等判断除了加大计算量之外，没有实际意义。此时，则可根据实际精度需求确定允许误差，然后用允许误差替代数据误差进行相等判断。这种方法更简单，而且允许误差一般远大于数据误差，可以减小计算量。不过，所谓的允许误差往往没有确定的值，主要依据经验来判断，因此有较大的不确定性。 虽然相对于“==”操作符，使用if(fabs(a-b) < epsilon)形式进行判断是一个比较好的解决方案，但它却存在着一定的局限性。比如，epsilon的取值为0.0001，而a和b的数值大小也在0.0001附近，那么它显然是不合适的。另外，对于a和b大小是10000这样的数据，它也不合适，因为10000和10001也可以认为是相等的。 既然这种绝对误差形式“if(fabs(a-b) < epsilon)”存在着局限性，那么我们可以尝试使用相对误差的形式“fabs ( (a-b)/a ) < epsilon”进行判断，示例代码如下所示：

bool IsEqual(float a, float b, float epsilon ) {       return ( fabs ( (a-b)/a ) < epsilon ) ? true  : false; }

这样的判断形式看起来是可行的，但它同样存在着局限性。因为它是拿固定的第一个参数做比较的，如果我们分别调用IsEqual(a, b, epsilon)和IsEqual(b, a, epsilon)，那么可能会得到不同的结果。与此同时，如果第一个参数是0，很可能会产生除0溢出。因此，我们可以把上面的判断形式改造为：除数选取为a和b当中绝对数值较大的即可，示例代码如下所示：

bool IsEqual(float a, float b, float epsilon ){     if (fabs(a)>fabs(b))     {            return  ( fabs((a-b)/a) < epsilon ) ? true : false;    }    else    {            return  (fabs( (a-b)/b) < epsilon ) ? true : false;    }}

这样看起来就更加完善了。当然，在某些特殊的情况下，相对误差也不能代表全部。因此，我们还需要将相对误差和绝对误差结合使用。完整的比较示例代码如下所示：

bool IsEqual(float a, float b, float epsilon ) {     if (a==b)     {            return true;     }    if (fabs(a-b)
    
     fabs(b))     {            return  ( fabs((a-b)/a) < epsilon ) ? true : false;    }    else    {            return  (fabs( (a-b)/b) < epsilon ) ? true : false;    }}